Each of these techniques has its advantages and disadvantages, and the choice will depend on the microfluidic application. Ultimately, measuring shear stress accurately can help scientists better understand cell behavior under flow conditions.
What Is The Definition Of Shear Stress?
Shear stress is defined as the stress created when a tangential force acts on a surface. The definition of shear stress applied to biology and microfluidics is the frictional force of a biological fluid flow acting on cells or tissues.How to Determine Shear Stress?
Fluid shear stress increases with fluid velocity and with viscosity, therefore for Newtonian fluids it may be computed according to Newton’s law with the following relation^{1}:\tau =\eta \frac{\partial v}{\partial z}
where \eta viscosity is the viscosity (g/cm-s = Poise)\frac{\partial v}{\partial z} is the velocity gradient or shear rate (s^{-1}), In the SI system, unit is Pascal (PA) but in the cardiovascular system another unit is often used: dyn/cm2 (1Pa= 10 dyn/cm2).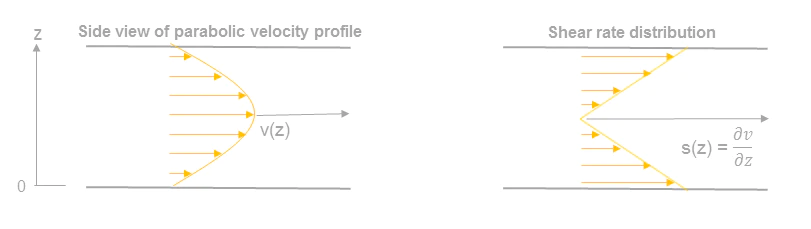
The fluid flow does not have the same velocity at every point in the channel, creating a velocity distribution with a velocity profile that tends to be parabolic in most simple cases of laminar flow. Fluid velocity is the fastest at the center and slowest near the channel wall. When z=0, the shear stress created by the fluid is referred as the “wall shear stress” and the velocity gradient is usually called “wall shear rate”. Wall shear stress order of magnitude is usually the highest value in the channel. When experimenting with adherent cells or wanting to avoid shear stress detrimental effects, the wall shear stress value is usually the one used.
When setting up a biology experiment with microfluidics it is crucial to consider shear stress. The final goal can either be to avoid shear stress, and reduce it to its minimal value to avoid cell deterioration and even cell death or it can also be to mimic the in vivo shear stress to study physiological processes such as the impact of mechanical stresses on cells.
In order to reproduce a biological process, it’s important to know what’s happening in vivo. Numerous articles have been describing this phenomenon and the in vivo consequences.
In vivo shear stress
Wherever there is flow, shear stress exists. In vivo, shear stress is mostly due to the frictional force of blood flow against the vessel walls. In our body, some cells are continuously under shear stresses such as endothelial cells and kidney epithelial cells but flow patterns are not uniform in the vascular system^{2}:
- In veins and small arteries: Generally laminar & High wall shear stress are mostly observed
- In branches and curvature: Disturbed flow pattern & Low wall shear stress
The hemodynamic forces and the resulting mechanical stress have numerous biological responses that were well identified over the last decades. The first observable impact is a change of morphology as the cells are elongated in the direction of the flow. After exposure to shear stress, there is also a clear reorganization of the cytoskeleton^{3}, the alignment of microtubules and a change of actin distribution.
For example, shear stresses have been shown to alter gene expression, to regulate activation of signaling pathways and to have some impact on calcium uptake, differentiation, proliferation and protein expression. When shear stress increase, proliferation mechanisms are activated.
Furthermore, vascular remodeling processes can be observed with an expansion of the vessel’s diameter and an increase of the wall thickness^{4}. On the contrary, low shear stress values will lead to a reduction in vessel’s diameter.
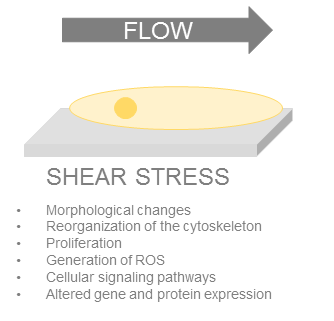
Cell behavior under shear stress have been described in many articles. Depending on the cell line, the impact can be different. For stem cells, it can induce differentiation and for endothelial cells (ECs), shear stress has a huge impact on the phenotype and it can even lead to some pathologies.
For example in regions with oscillating shear stress, it can lead to pathologic changes in the artery walls and it increases the risk of atherosclerosis^{5}. Shear stress alteration can also have a role in aneurysms due to the synthesis of reactive oxygen species (ROS), Nitric oxyde (NO), growth factors and metalloproteinase.
Shear stress has an important role in various biological processes at the molecular and clinical level. Mechanical forces are sensed by the cells and it leads to mechanotransduction into biological responses. Below, a summary of the different effects described in the literature depending on the flow pattern and shear stress:
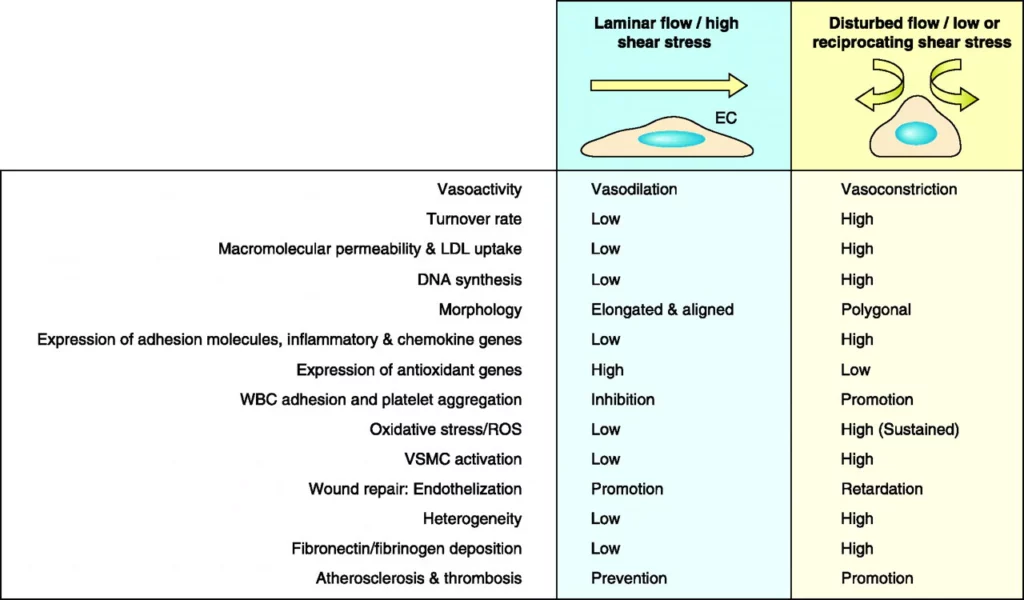
Average values of shear stress in human arteries with basal conditions are around 2-20 dyne/cm². It’s important to point out that even at a shear stress as low as 4 dyne/cm², morphological changes are observed in vivo. Much higher values^{6} (from 30 to 100 dyne/cm²) can be observed near arterial branches and strong curvature such as aortic arch, bifurcations whereas much lower values from 1 to 6 dyne/cm² are usually measured in veins.
In vitro shear stress
In conventional 2D cell cultures, cells are not exposed to mechanical forces such as shear stress, tension and compression which have an impact on organ development and function.
For example, when there is no fluid flow, the interaction between the studied cells with blood and immune cells can’t be evaluated. It’s a huge limitation of cell culture studies.
Therefore, the use microfluidics device is a viable alternative to traditional in-vitro techniques because of its physiological relevance. Microfluidics can provide a 3D biomimetic microenvironment and more recently it is even used to do organs on a chip in order to mimic in vitro organs. Those applications are closer to what is happening in-vivo but the new challenge is to take into account mechanical forces such as shear stress.
In microfluidic devices, shear stress is created by the fluid flow injection. Due to the small dimensions of microfluidics devices, flow is laminar, consequently, it’s a good way to mimic flows found in veins and small arteries where the flow is usually unidirectional and laminar^{7}. In larger arteries, flows encountered are often pulsatile and laminar. In a microfluidic experiment, flow rate can be changed periodically to mimic this flow type.
In general, most flow patterns can be mimic with microfluidics as the only exception is turbulent flow which is rarely found within biological systems. Microfluidics experimentation is therefore a good in-vivo approximation^{8}. On the other hand, shear stress can also be seen has a drawback due to the inherent detrimental effects observed at high level. Fortunately, it is possible to design a microfluidic experiment such that shear stress won’t have unwanted effects.
In both situations: investigation of a biological phenomena or when shear stress is seen as a limitating factors, it’s crucial to take time and take into account some parameters when designing the experiment.
Microfluidics and shear stress in cell experiments
Among all the things to consider when designing a microfluidics experiment, the level of shear stress experienced by the cells is a physiologically important concern. In microfluidics devices several parameters will have influence on shear stress: dimensions and geometry of the channels, cell concentration, type of cell line, the way flow rate is delivered, etc. Some of the mentioned parameters will be described with more details in order to understand how to control and measure shear stress in microfluidic devices.
Designing a microfluidics experiment
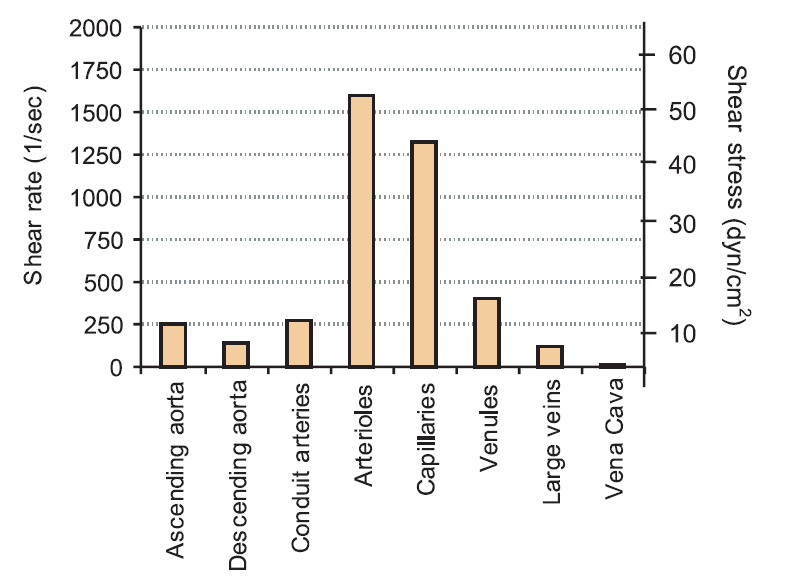
Mimicking in vivo shear stress: experimental values
In experiments where static and biomimetic conditions are wanted, the value used is between: 0.2 and 0.5 dyne/cm². In order to mimic the flow through a certain type of vessel, the indicated values of shear stresses and shear rates below can be used as a reference:
Choice of cell lines
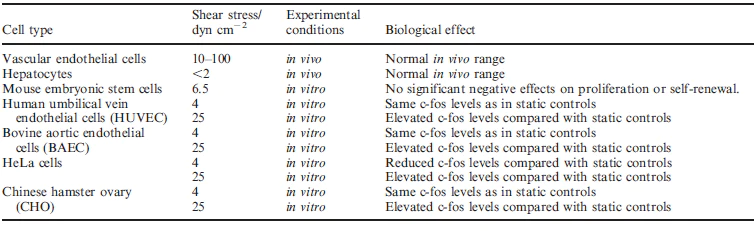
Cell responses to shear stress and their ability to resist to fluid forces are dependent on cell types. In some studies different cell types under the same conditions have been observed, and it led to the conclusion that there is a wide range of responses to shear stress depending on the cell used. One step of the design experiment is to find out which cell lines should be used and which flow rate should be applied depending on the wanted outcome.
Chips design
In any fluid system, the ability to predict shear stress is of great importance to predict the consequences on cells phenotype^{11}. Hence, when designing an experiment and a new microfluidic chip, shear stress can be calculated or modeled.
Choice of the flow control system
In microfluidics and cell experiments it’s crucial to get precise and smooth flow control. It’s a key parameter to control shear stress and consequently, the choice of flow control instrument is important.
Several options are existing such as syringe pumps, peristaltic pumps, or pressure control systems with or without flow switches. Each of these systems has its advantages and drawbacks and the choice will depend on the microfluidic application. The following review elaborates more on the relative advantages and disadvantages of popular flow control methods.
When dealing with shear stress, there are major drawbacks to avoid: low response time, unwanted flow rate oscillations, and uncontrollable fluctuations. These drawbacks can lead to a major difference between the calculated/simulated flow rate and the real one. In order to get a flow rate as close to what is wanted, a fast response time, and accurate flow control, a pressure control system may be one of the best solutions on the market.
How To Measure Shear Stress?
Evaluating the shear stress in a cell culture under flow can be done in multiple ways. The shear stress can be evaluated using fluid dynamics theoretical and numerical methods. In order to calculate the flow, thus the shear stress, in a microfluidic setup, one has to solve the Navier-Stokes equation, either numerically or analytically to find the velocity profile for the considered geometry. In the case of simple geometries such as a wide rectangular channel or a tubular channel, the analytic solution is simple and can be found in the literature. For instance, for a rectangular canal of dimensions w*h*l with h>w>>l, the wall shear stress can be computed as \tau=\frac{6\eta Q}{h²W} with Q the flowrate. For a cylindrical channel the shear stress is \tau=\frac{4\eta Q}{R^{3}}/\pi.
However, these simple formulas does not represent the shear stress for complex geometries where it is generally better to perform a computer simulation to estimate the shear stress or the shear rate.
These calculations are really useful to estimate, even precisely, the shear stress. However, when one wants to know the shear stress experimentally as best as possible in a microfluidic experiment, several methods allowing for local measurement or estimation of the shear stress in the region of interest can be used. We have developed a simple (but handy) tool to help you determined the approximate pressure in your chip.
For investigation in cell cultures, measuring the shear stress as close as possible to the cells can be desired. There are several sensing methods to do so.
Cell based sensor
Flow shear stress leads can lead to activation to some signalization pathway^{12}. One method that has been developed to measure shear stress is genetically encoded fluorescent cell sensors reacting to flow shear stress pathway activation.
Liquid crystal
Potential use of liquid cristals as a shear measurement technique have been shown in microfluidic devices^{13}. This experimental technique is based on the properties of liquid cristals and their chiral molecular structures. When shear stress is applied, the structure of molecules bends which can lead to a change in polarization or wavelength that can be measured.
Micro particle velocimetry
Micro particle velocimetry (µ-PIV) systems can be used to get an accurate readout of the wall shear stress that can also resolve the cells surface directly^{14}. This allows to measure the flow profile to determine the shear stress. A µ-PIV system consists of a high speed camera synchronized with a double cavity laser that illuminates particles introduced in the liquid flow and monitors their position with high accuracy. Such system are really powerful, but the complexity of their implementation makes them unfit for easy shear stress measurement.
Laser Doppler Velocimetry
Another way of measuring velocity profiles in liquid flows close to the interface is to use Doppler shift of laser light^{15}. Here, Doppler shift a laser light reflected inside the flow is monitored in order to measure the flow profile of the liquid and determine the shear stress. The apparatus for such measurement is simpler than for the image velocimetry as the laser does not have to be synchronized with a camera and one just needs to measure its frequency shift, but the process is less documented and the results are not as precise.
Nevertheless, this is a really promising alternative for low-cost flow measurement and shear stress evaluation closer to the cells.
Bibliography
- Transport phenomena, R. B. Bird, W. E. Stewart, and E. N. Lightfoot, John Wiley and Sons, Inc., New York(1960). 780 pages.$11.50. (1961). AIChE Journal, 7(2), pp.5J-6J.
- Chiu, J. and Chien, S. (2011). Effects of Disturbed Flow on Vascular Endothelium: Pathophysiological Basis and Clinical Perspectives. Physiological Reviews, 91(1), pp.327-387.
- Malek, A., Izumo S. (1996). Mechanism of endothelial cell shape change and cytoskeletal remodeling in response to fluid shear stress. J Cell Sci, (Pt 4):713-26.
- Glagov, S., Zarins, C. and Giddens, D. (1994). Hemodynamics, the structure of the artery wall and atherosclerosis. Atherosclerosis, 109(1-2), p.343.
- Davies, P. (2008). Hemodynamic shear stress and the endothelium in cardiovascular pathophysiology. Nature Clinical Practice Cardiovascular Medicine, 6(1), pp.16-26.
- Dewey, C., Bussolari, S., Gimbrone, M. and Davies, P. (1981). The Dynamic Response of Vascular Endothelial Cells to Fluid Shear Stress. Journal of Biomechanical Engineering, 103(3), p.177.
- Franklin, K. J. (1937). Veins and the nervous system. In “A Monograph on Veins” (K. J. Franklin, ed.), Chapter 10.
- Freund, J., Goetz, J., Hill, K. and Vermot, J. (2012). Fluid flows and forces in development: functions, features and biophysical principles. Development, 139(16), pp.3063-3063.
- Papaioannou TG(1), Stefanadis C. (2005) Vascular wall shear stress: basic principles and methods. Hellenic J Cardiol 46(1):9-15.
- Kim, L., Toh, Y., Voldman, J. and Yu, H. (2007). A practical guide to microfluidic perfusion culture of adherent mammalian cells. Lab on a Chip, 7(6), p.681.
- Barber, R. and Emerson, D. (2007). Optimal design of microfluidic networks using biologically inspired principles. Microfluidics and Nanofluidics, 4(3), pp.179-191.
- Varma, S. and Voldman, J. (2015). A cell-based sensor of fluid shear stress for microfluidics. Lab Chip, 15(6), pp.1563-1573.
- Martel, J., Bradford, A. Bruno, (2008). Shear stress measurement in Microfluidic systems: Liquid Crystal Technique. ASME, pp. 2009-2018; 10 pages
- Rossi, M., Lindken, R., Hierck, B. P., & Westerweel, J. (2009). Tapered microfluidic chip for the study of biochemical and mechanical response at subcellular level of endothelial cells to shear flow. Lab on a Chip, 9(10), 1403-1411.
- Campagnolo, L., Nikolić, M., Perchoux, J., Lim, Y. L., Bertling, K., Loubiere, K., … & Bosch, T. (2013). Flow profile measurement in microchannel using the optical feedback interferometry sensing technique. Microfluidics and Nanofluidics, 14(1-2), 113-119.